经过青岛创统科技研发团队的共同努力，研发设计出网侧电流检测算法：

1.小波神经网络的结构

小波神经网络(WNN)是小波分析理论与人工神经网络理论相结合的产物，从结构形式上可分为小波变换和神经网络的松散型结合与紧致型结合两大类，若采用紧致型小波神经网络^[3-4]， 设x=[x₁，x₂， …， x_n]^T为输入向量，y=[y₁，y₂， …，y_m]^T为输出向量，输出层到隐层的权值为w_ij，隐层到输入层的权值为w_jk，中间隐层的伸缩参数和平移参数分别为a_j和b_j，若隐层神经元数为N，则i=1，2，…，m，j=1，2，…，N，k=1，2，…，n，其网络方程的实现可表示为：

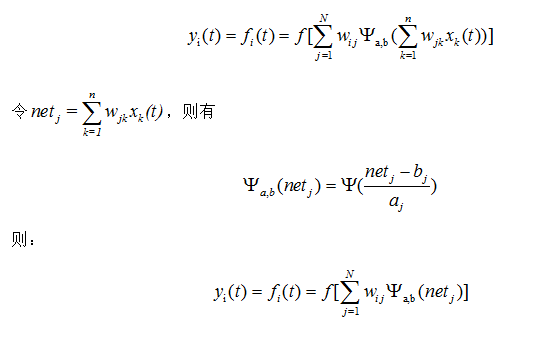
2.小波神经网络的学习算法

在小波网络进行训练之前，小波基函数的选取，以及小波基个数的多少，都将直接影响到估计精度和计算的复杂程度，根据PWM整流器的数学模型特点选取 Morlet小波函数:

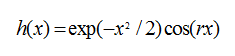
它是 Gauss函数的二阶导数，在时域和频域都有很好的局部特性。一般r取1.75，共有N组训练样本对(x(n)，y(t_n))，n = 1，2 ，…，N。采用学习速率自适应调整的BP算法训练小波神经网络，训练时采用批量处理。取优化目标函数为：

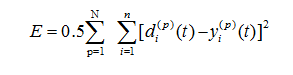
整流器电流采样的特点决定了网络的输入节点数和输出节点数，因此选择网络规模主要是确定隐层节点数的大小。小波神经网络的训练学习和隐层节点数密切相关，隐层节点数过少，网络不能具有必要的信息处理能力和学习能力，隐层节点数过多，增加了网络结构的复杂性，在学习过程中更容易陷入局部最小，而且使网络的学习速度变慢。常用的试凑法一般是根据经验来选取隐层的节点数，有很大的随机性。采用下述经验公式来确定神经网络隐层节点数：

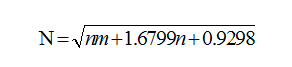
n为输入节点数，m为输出节点数。

采用梯度下降法，调整网络参数，得到相应的最优参数：

1）网络参数的初始化：w_ij设为0，中间隐层的伸缩参数和平移参数分别为a_j和b_j，选取计算样本重心的方法，即为了初始化a₁和b₁，先在[0，n] 上选择一个p点, 该点为[0，n]区间的重心, 设a₁=p,b₁=ξ(n-0)=ξn(一般ξ=0.5),这样点p把区间[0,n]分成两部分,然后可以在这两个区间上重复以上步骤，就可以初始化参数a₂和b₂,直到a_N和b_N；

2）输入学习样本对(X(p),Y(p))；

3）网络的自学习：利用当前的网络参数计算出网络的输出；

4）计算瞬时梯度向量和增量：

      各梯度项为：

式中:η_ij，η_jk，η_a，η_b 分别为参数w_ij，w_jk，a_j，b_j 的学习速率。

 （5）当E小于容许误差或达到最大学习次数时，终止学习；否则返回步第(2)步。